Fysica van ruimte-tijd deel II, meters en seconden

II.1. De overbodige maatstaven gram en coulomb

Een belangrijke taak van de natuurkunde is meten van de verschijnselen in de werkelijkheid, om vervolgens die fenomenen op een wiskundige manier te beschrijven. En natuurlijk heeft men dan ook maatstaven nodig om die grootheden in uit te drukken.

Omdat er vele verschillende natuurkundige verschijnselen bestaan, zijn er ook vele verschillende maatstaven in de natuurkunde, net als in het dagelijkse leven. We meten ruimte en tijd, snelheid en versnelling, gewicht, temperatuur, druk, energie, allerlei elektromagnetische verschijnselen enzovoort. En voor elk verschijnsel hebben we een maatstaf als de meter, de seconde, de kilogram, de graad, de watt, de ampère, de volt enzovoort.

Toch zijn bijna al die verschillende maatstaven te herleiden tot maar 4 maatstaven, de meter (m) voor ruimte, de seconde (sec) voor tijd, de kilogram (kg = 1000 gram) voor massa en de coulomb (C) voor elektrische lading. Andere maatstaven zijn opgebouwd uit een combinatie van die vier of enkele van die vier. Zo is snelheid meters per seconde, stroomsterkte (ampère dus) het aantal coulombs per seconde, energie (joule) een product van kilogram en snelheid in het kwadraat enzovoort.

De werkelijkheid is veel eenvoudiger dan de beschrijving van de wetenschap. Alles wat je ziet en ervaart is niets meer dan een ruimte-tijd relateren tussen neutronen, protonen en elektronen. Die deeltjes hebben allemaal een massa, terwijl protonen en elektronen ook een lading hebben. En wat je ook ziet, hoort, proeft, ruikt, ademt of voelt, je ervaart altijd een relateren tussen die fundamentele deeltjes.
Die deeltjes bewegen in ruimte en tijd en dan voelen we ons lichaam, voelen warmte of de wind, of we zien dan kleuren, proeven of ruiken voedsel, horen muziek of lawaai, zien plaatjes op een scherm enzovoort.
Massa en lading bewegend in ruimte en tijd, dat is alles wat er is, wat betreft de kwantiteit dan, de kaart dus die de natuurkunde maakt.

De vier basis-maatstaven zijn dus: m, sec, kg en C. Die kunnen alles beschrijven, samen met cijfers natuurlijk.
En zelfs die kg en C kunnen we eigenlijk missen, en dat te laten zien is het doel van dit deel II. Het gevolg is dan een natuurkunde van ruimte en tijd, een natuurkunde die in mijn ogen perfect past bij de moderne inzichten, waarin massa zijn absolute karakter verloren heeft.

Waarom zijn de kg en de C overbodig? Laat ik beginnen met de coulomb.
Toen mensen elektriciteit ontdekten, wisten ze er natuurlijk nog niet veel van af. Men kende bijvoorbeeld het elektron nog niet als bron van lading, als kleinste lading-eenheid.
Een tamelijk willekeurige hoeveelheid lading is men toen een lading van 1 coulomb gaan noemen . Een lading is 1 C als het een kracht van 9×10⁹ newton (= kg×m/sec²) teweeg brengt op een even grote lading op 1 meter afstand, in de lege ruimte.

Tegenwoordig weten we dat er een kleinste lading bestaat, de lading van een elektron die even groot is als de tegengestelde lading van een proton. Een hoeveelheid lading is altijd een geheel aantal elektronen; te veel elektronen noemen we een negatieve lading, te weinig elektronen een positieve lading. En halve elektronen bestaan niet.

Er bestaat dus een echte eenheid van lading in de werkelijkheid, het elektron. Als we vrij zouden zijn om de maatstaf voor lading nu te kiezen, dan zouden we ongetwijfeld die natuurlijke eenheid als maatstaf kiezen.
Waarom gebruiken we nog steeds zo'n kunstmatige en duistere maatstaf als de coulomb, als er een echte natuurlijke maatstaf bestaat? Omdat we er aan gewend zijn, lijkt mij.
Praktische overwegingen kunnen ook een rol spelen. Want als we echt het elektron als nieuwe maatstaf gaan hanteren, dan zouden, op het eerste gezicht, miljoenen meetinstrumenten moeten worden vervangen en dat zou miljoenen kosten. Echter als we het slim aanpakken, hoeft er niet veel te veranderen in de praktijk, maar daarover straks.

Eerst de theorie. Zoals ik al schreef, als we nu de maatstaf voor lading zouden kiezen, zouden we ongetwijfeld het elektron als maatstaf kiezen bijvoorbeeld door zijn lading 1 coulomb te noemen.
Maar als we zeggen dat 1 elektron een lading van 1 coulomb heeft, wat bedoelen we dan met het woord coulomb?
Eigenlijk betekent coulomb dan precies hetzelfde als kleinste lading of elementaire lading of gewoon lading. En omdat we met coulomb dan lading-eenheid bedoelen, kunnen we de lading van 1 elektron dan ook beter gewoon 1 lading-eenheid noemen in plaats van coulomb. Door de lading coulomb te noemen, geven we geen extra informatie. Integendeel, we verdoezelen dan informatie; het lijkt dan alsof coulomb iets betekent.

Dus laten we de lading van 1 elektron = 1 lading-eenheid noemen of gewoon 1 lading. Grotere ladingen worden dan een geheel aantal ladingen.
We drukken dan de werkelijkheid veel nauwkeuriger en duidelijker uit dan door te zeggen dat de lading van 1 elektron = 1,602×10^-19 C zoals we nu doen. En een lading van 1 C wordt dan een lading van 6,2422×10¹⁸ lading-eenheden zoals ook werkelijk het geval is.

1 elektron = 1,602×10-19 C, is als 1 mens = 1,602×10-10 mensheid.

We weten dat aantal dan niet exact, dus niet alle 18 cijfers achter de komma. Maar dat is ook zo als we dat aantal 1 C noemen.
We kunnen het aantal exact maken, gewoon door af te spreken dat we met 1 C voortaan exact 6,2422×10¹⁸ lading-eenheden bedoelen, of 6,24×10¹⁸. Het probleem is dan een praktisch probleem, het probleem om precies 6.240.000.000.000.000.000 elektronen af te wegen.

Het zou dus verstandig zijn om de maatstaf coulomb te vervangen door het aantal lading-eenheden waar die coulomb eigenlijk voor staat. Overal waar we C in de natuurkunde tegen komen, kunnen we C dus vervangen door 6,2422×10¹⁸ lading-eenheden. Lading-eenheid zouden we dan kunnen aanduiden met een letter of ander symbool.

Maar als je zegt dat de lading van 1 elektron = 1 lading-eenheid, dan kan je die lading natuurlijk ook gewoon uitdrukken als 1, als een getal dus. Ik bedoel, we hebben al gezegd dat we het over lading hebben, dus waarom dat woord lading nog eens herhalen? Als ik zeg "Het aantal mensen is 10." dan is volkomen duidelijk wat ik bedoel. Men hoeft niet te zeggen "Het aantal mensen is 10 mensen.".
Men hoeft niet te zeggen dat de lading X ladingen is. De lading is X, dat zegt genoeg. Lading is een aantal, een getal.

We kunnen dus de maatstaf coulomb elimineren en vervangen voor het aantal dat in feite wordt bedoeld, zonder daardoor informatie te verliezen. Integendeel, we winnen dan informatie; kinderen leren dan vanzelf dat lading bestaat uit kleinste deeltjes.

En dat is ook alles wat we weten. Wat is lading precies? Dat weten we niet, dat kunnen we niet nader verklaren. We weten dat lading kan bewegen, eigenlijk altijd beweegt, en die beweging kunnen we dan meten als warmte, als licht, als energie en dergelijke. En energie en dergelijke bestaan dan uit kleinste pakketjes, omdat de werkende lading uit kleinste deeltjes bestaat.
Dat is alles wat we meten, dus een beweging in ruimte en tijd die bestaat uit kleinste pakketjes. Wat is lading? Een potentiële ruimte-tijd beweging, dat is alles wat we weten.

Nu over de praktische consequenties. Moeten we al onze meetinstrumenten weg gooien als we C vervangen door een getal?
Nee, omdat we het woord coulomb gewoon kunnen blijven gebruiken, maar dan als aanduiding voor een getal, zoals kilo 1000 betekent. C wordt dan het getal 6,2422×10¹⁸. Dan kunnen we onze oude meetinstrumenten gewoon blijven hanteren. De verandering is dan slechts een verandering in de theorie.

En ook nu betekent het begrip coulomb niets meer dan dat getal, dat aantal. Dus laten we eerlijk zijn en het symbool C vervangen door het getal 6,2422×10¹⁸. Dat is echt alles wat we weten.

Eenzelfde beschouwing kan worden gehouden over de kilogram, de maatstaf voor massa, alhoewel hier een probleem lijkt te bestaan omdat we 3 fundamentele massa-deeltjes kennen, het neutron, het proton en het elektron. Maar ik denk dat dat niet echt een probleem is. Een geïsoleerd neutron valt na verloop van korte tijd vanzelf uiteen in een proton plus een elektron, wordt dus een waterstofatoom. Een neutron omvat dus in zekere zin het proton en het elektron.

We zouden in elk geval het neutron als maatstaf voor massa kunnen kiezen, in plaats van dat willekeurige stuk staal of wat dan ook in Parijs of waar dan ook. Dat zou echt een verbetering zijn omdat we dan een natuurlijke maatstaf hanteren.
Het begrip kilogram zou dan gaan betekenen een aantal massa-eenheden, een equivalent aantal neutronen, en in feite is dat ook werkelijk zo. In theorie kan elk brok materie herleid worden tot een geheel aantal neutronen, mits het stuk materie elektrisch neutraal is. Is het ding geladen dan blijven we ook zitten met wat protonen of wat elektronen.

De massa van 1 neutron zouden we dus 1 massa-eenheid kunnen noemen of gewoon 1 massa. Maar als je zegt “de massa van 1 neutron = 1 massa“ dan kan je natuurlijk dat tweede gebruik van het begrip massa gewoon weg laten. De massa van 1 neutron = 1, dat zegt genoeg.

Massa wordt dan een aantal, en dat is ook alles wat we er van weten.
Wat is massa? Massa kan ook alleen maar worden gemeten als beweging, als gewicht, als warmte, als wind, als kracht, als energie. Meten zelf is ook zo'n beweging, meten is wegen.
En die bewegingen hebben dan altijd een pakketjes-karakter. Men kan een gewicht of een hoeveelheid energie niet oneindig blijven splitsen in almaar kleinere pakketjes. En dat komt omdat de werkende massa uit kleinste deeltjes bestaat.

De maatstaf kilogram kan dus evenals de coulomb worden geëlimineerd. Ze moeten zelfs worden geëlimineerd, vind ik, omdat ze volstrekt overbodig zijn terwijl er in een exacte wetenschap als de natuurkunde geen plaats is voor overbodigheden.
En ook nu heeft het begrip gram geen enkele andere betekenis dan een aantal, een getal. Dus laten we eerlijk zijn en dat aantal hanteren in plaats van een duister begrip als gram, alsof gram iets betekent .

En ook hier zou het wijs zijn om het begrip gram te blijven gebruiken, echter met dit verschil dat het begrip voortaan een getal aan duidt. Een kg wordt dan het getal 5,9712×10²⁶, 1 gram dus het getal 5,9712×10²³, zelfs exact dat getal als we dat afspreken, of het getal 6×10²³.

Ik kan echt geen enkel argument bedenken tegen eliminatie van de gram en de coulomb. Een praktisch argument ook niet, als we die begrippen blijven gebruiken als aanduidingen voor getallen, zodat we al onze oude meet-instrumenten kunnen blijven gebruiken.
Ik zie alleen maar voordelen, voor onze kinderen bijvoorbeeld die dan automatisch leren dat massa en lading altijd bestaan uit kleinste eenheden.

En natuurkunde wordt dan natuurkunde van ruimte en tijd, waarin alles wordt uitgedrukt in termen van slechts meters en seconden, en getallen natuurlijk ook. Zo'n natuurkunde past perfect bij de moderne inzichten.

Het bestaan van kleinste eenheden van massa en lading wordt dan zichtbaar in de natuurkunde in de vorm van kleinste lengtematen en/of kleinste tijdsbestekjes, fundamentele ruimte-tijd eenheden.

Dus wat gebeurt er in de natuurkunde?
Als kg en C getallen worden, dan krijgen andere maatstaven ook een nieuwe betekenis.
1 J (joule) = kg×(m/sec)² dan = 5,9712×10²⁶ (m/sec)²
1 A (ampère) = C/sec dan = 6,2422×10¹⁸ sec^-1
1 V (volt) = J/C dan = 9,5659×10⁷ (m/sec)²
1 (ohm) = V/A dan = 1,5325×10^-11 m²/sec

Overal in de natuurkunde waar we C, kg, J, A, V en tegen komen, kunnen we die symbolen vervangen door die nieuwe uitdrukkingen in getallen, meters en seconden.

En ook hier kunnen we die symbolen J, A, V en blijven gebruiken, met name in de praktijk, maar met een nieuwe betekenis. 1 A is dan een aantal per seconde, 1 is een aantal maal een lengte maal een snelheid, terwijl 1 J en 1 V aantallen zijn maal een snelheid in het kwadraat.
J drukt mechanische energie uit en dan speelt altijd een aantal massa-eenheden een rol. V is de energie per lading, een aantal van de massa-eenheden is dan ook lading-eenheid. In is de lading-massa verhouding het aantal massa-eenheden per het kwadraat van het aantal lading-eenheden.

De informatie over die massa- of lading-aantallen en over de relatie tussen die aantallen zit verborgen in de woorden gewicht, energie, stroomsterkte, spanning, weerstand en dergelijke. Dus als we zowel de kg als de C vervangen door getallen, zullen natuurkundigen nooit in verwarring raken over welke aantallen een rol spelen. Als ze het bijvoorbeeld over spanning hebben, dan weten ze dat het gaat om het aantal massa-eenheden per het aantal lading-eenheden; kg/C is dan overbodig in de maatstaf, omdat kg/C al in het begrip spanning zit.

Dus laten we C, kg, J, A, V en vervangen door hun nieuwe uitdrukkingen.
Ik begin met h, de constante van Planck.
Deze h is zeer belangrijk in de quantum-natuurkunde, bijvoorbeeld in de formule E = h×f, waarin E de energie van licht is en f de frequentie van licht, het aantal golven per seconde.
De constante van Planck h = 6,625×10^-34 Jsec (joule×seconde).
Als we J vervangen door 5,9712×10²⁶ (m/sec)², dan verandert h in 3,9559×10^-7 m²/sec.
En als we m/sec zien als de lichtsnelheid c, houden we over een lengtemaat h/c = 1,3196×10^-15 meter die net zo fundamenteel is als h en c.
We kunnen h ook delen door c² en h/c² is dan 4,4017×10^-22 seconde.
Eigenlijk is h dat beroemde quantum dat voor het eerst ontdekt is door Max Planck. Het wezen van het quantum is dus blijkbaar een lengte (of een afstand).

Onze werkelijkheid is het gevolg van de eindigheid van onze lichtsnelheid en voor licht met een eindige snelheid bestaat er altijd een kleinste ruimtemaat, een kleinste golflengte bijvoorbeeld. Want als de golflengte oneindig klein zou worden, dan werd het licht zelf ook oneindig, zodat onze werkelijkheid dan onmogelijk werd.
Dus h is blijkbaar in de kern zo'n kleinste ruimtemaat die wij, de deeltjes, hanteren om elkaar te meten. En omdat ruimte niets anders is als meten en gemeten worden , vinden we die ruimtemaat, dat quantum, overal in de natuurkunde weer terug. Ook de afmetingen en zelfs de massa van de fundamentele deeltjes moeten (mede) bepaald zijn door die fundamentele lengtemaat.

Als tweede natuurconstante die voor komt in de wet van Coulomb, en die volgens de vergelijking van Maxwell afhankelijk is van de lichtsnelheid.
De constante = 8,8543×10^-12 Asec/Vm (= C/Vm).
Als we A (of C) en V vervangen door hun nieuwe uitdrukkingen dan wordt = 5,7778×10^-1 sec²/m³.
Ook daar kunnen we de lichtsnelheid uithalen, c² in dit geval, en dan verschijnt de lengte 1,9257×10^-17 meter die net zo fundamenteel is als of c.
Overigens is die lengte dan eigenlijk de magnetische constante .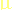
En 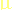= 1/c² volgens de vergelijking van Maxwell.

Overigens moet men dan geen waarde hechten aan de getalsgrootte van die lengtematen. Immers zouden we destijds een andere lengte 1 meter hebben genoemd, dan zouden ook de getalsgrootten van die fundamentele lengtematen anders zijn geweest.
De verhouding tussen die twee lengten is echter wel constant. Zouden we niet het neutron maar het elektron als massa-eenheid van 1 gaan hanteren, dan veranderen beide lengtematen in gelijke mate, zodat de verhouding ertussen gelijk blijft.

En h/c is 68,52 keer langer dan .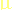
Dat verhoudingsgetal 68,52 (beter bekend als 2×68,5 = 137) moet een diepere betekenis hebben, lijkt mij. Alhoewel het heel goed mogelijk is dat dat getal niet verder rationeel kan worden verklaard, zoals het volgens mij ook onmogelijk is om het verhoudingsgetal (pi) verder te verklaren. Er moet dan een verhouding zijn, dat is zeker. Maar waarom precies dit getal? Daar is geen diepere reden voor lijkt mij.

Zien van nieuwe relaties heeft altijd meer eenheid tot gevolg, ook in een theoretisch systeem als de natuurkunde. En die nieuwe eenheid kan dan zelf ook weer nieuwe relaties zichtbaar maken enzovoort.
We zien nu bijvoorbeeld dat h in dezelfde combinatie van eenheden wordt uitgedrukt als weerstand tegen elektrische stroom, namelijk in termen van m²/sec, een lengte maal een snelheid.
Planck's constante h is dan ±25.813 ohm. En omdat h fundamenteel is, zou ±25.813 heel goed een fundamentele hoeveelheid weerstand kunnen zijn. En in 1980 ontdekte de Duitse natuurkundige Klaus von Klitzing inderdaad dat ±25.813 zich gedraagt als constante, een soort natuurlijke eenheid van weerstand.
De constante (weerstand van een vacuüm = 376,73 ) blijkt dan 1/68,52 deel van 25.813 ohm te zijn. Daar is dat getal 68,52 weer.

Weerstand, daar lijkt het allemaal om te draaien. En dat is natuurlijk ook het primaire kenmerk van een eindig snel licht, in vergelijking met een oneindig snel licht. Een oneindig licht heeft geen tijd nodig om ruimte te overbruggen. Ruimte heeft dan blijkbaar geen enkele weerstand. Een eindig snel licht echter ervaart weerstand, doet er immers tijd over om ruimte te overbruggen.
Zelfs lege ruimte heeft weerstand, voor een eindig licht. De niet lege ruimte, materie genoemd, heeft dan natuurlijk nog meer weerstand.

II.2. Meters, seconden en getallen

Natuurkunde is dan ruimte, tijd en getallen, dynamiek van ruimte en tijd.
Maar die natuurkunde is natuurlijk niet meer dan een kaart van het gebied en niet de werkelijkheid. In de werkelijkheid is alles afstand, dus ruimte en tijd in een. Ruimte is alleen ruimte als het een betekenis heeft en die betekenis wordt altijd ervaren als de tijd die erover wordt gedaan, ook in muziek trouwens en in kleur.
Op de kaart echter kunnen we die eenheid van ruimte-tijd niet in maar 1 cijfer uitdrukken. Daar, op de kaart, moeten we afstand op splitsen in ruimte los van tijd.

Eigenlijk is het de tijd die we niet kunnen vatten. We kunnen tijd-stippen meten maar niet de tijd zelf. Tijd speelt altijd ongrijpbaar tussen twee tijd-stippen, hoe kort we het interval ook maken tussen twee tikken. Dat interval kan nooit nul worden, want dan bestaat er in het geheel geen tijd meer. Dus hoe meer we tijd proberen te vatten, door de intervallen almaar korter te maken, des te meer ontglipt ons tijd .

De kaart van de natuurkunde is niet meer dan een moment-opname, zoals elke kaart. Natuurkunde is dus niet alleen maar begrijpen van de cijfers op de kaart, maar ook een juiste interpretatie van de kaart, als niet meer dan een abstractie, een moment-opname waarop de tijd stil staat.
De tijd moeten we zelf invullen als we de kaart lezen, zoals we het idee van de schroefdraad in vullen als we een bout-moer koppel zien.

En een juiste interpretatie van de kaart zelf als slechts een kaart, is eigenlijk ook een juiste interpretatie van onze geest. En dat, begrijpen van onze geest, is ook het voornaamste doel van de Relationele filosofie.

II.3. De werkelijkheid als relateren tussen nul en oneindig

Nog een maal terug naar de natuurkunde. Zullen we ooit in staat zijn het proton en het elektron en wat tussen hen speelt echt te begrijpen?
Echt begrijpen betekent altijd dat je het begrepene als het ware kunt schetsen. We kunnen de bout en de moer tekenen en de man en de vrouw. De relaties hebben dan een tastbare vorm nodig om zich te kunnen uit drukken.
Echter, een proton en elektron zijn in zekere zin alleen maar afmeting, zonder concrete vorm, een soort vormloze vorm. En hoe kunnen we dat tekenen? Omvatten en omvat worden zonder iets?

Toch kunnen we er wel aan denken en dan begrijpen dat zulke zuivere vormen inderdaad mogelijk kunnen zijn. Het is als met wiskunde met meer dan de 3 ruimte-dimensies die we in de praktijk kennen. We weten in elk geval wat een dimensie is, en we kunnen zelfs een 2-dimensionale wereld schetsen. En daarom kan ook een 4-dimensionale wereld mogelijk zijn in onze gedachten. Vanuit die 4-de dimensie zou je dan onze 3-dimensionale wereld zien, zoals wij kijken naar wezens die denken dat er slechts 2 dimensies bestaan.
Wij weten dan wel beter, zien wat de 2-dimensionalen niet zien. En zo zou er best een nog beter weten kunnen bestaan, niet te vatten voor ons 3-dimensionalen.

We kunnen het niet schetsen. Toch kunnen we het beeldend begrijpen.
Op dezelfde manier kunnen we het proton en elektron beeldend begrijpen. En de concrete vormen van bout en moer of van man en vrouw kunnen ons dan zelfs behulpzaam zijn.
Al die relaties moeten immers familie van elkaar zijn, simpel omdat alles uiteindelijk gemaakt is van protonen en elektronen en wat tussen hen speelt. Alle mogelijke relaties moeten daarom hebben bestaan in dat eerste proton-elektron paar, als een potentie en dat is ook iets.

En om echt te kunnen begrijpen, moeten we ons ook realiseren dat die niet materiële relaties het echte fundament zijn van de werkelijkheid, ook van materie. Als we een bout en moer kopen, dan betalen we voor het materiaal. Echter in feite kopen we de niet materiële relatie, immers zouden bout en moer aan elkaar gelast zijn, dan kochten we het materiaal niet. Het draait altijd om die niet materiële relaties.
Op een fundamenteel niveau bepalen die niet materiële relaties zelfs het materiële van proton en elektron. Dat moet zo zijn omdat een deeltje niet kan bestaan zonder relatie. Een deeltje is een relatie, een deel in relatie tot alles, of in relatie tot niets.

Maar wat is dan die fundamentele relatie die materie schept uit het niets?
Voor een oneindig snel licht zijn een nulpunt van niets en de oneindigheid van alles precies hetzelfde, allebei helemaal niets. Voornaamste eigenschap van eindig snel licht is echter dat het nooit een nulpunt van niets kan bereiken en evenmin de eeuwige oneindigheid. Daarom ook is het eindig.
Voor alles maakt een eindig licht dus een verschil tussen nul en oneindig, met als gevolg alle eindige maten ertussen. Een eindig licht is dus iets dat voortdurend zweeft ergens tussen nul en oneindig, tussen niets en alles, een niet materiële sfeer rondom niets. Een gespannen sfeer ook, iets betrekkelijks, een relateren.
Voor zo'n sfeer is er dan in elk geval een verschil tussen iets als binnen-ruimte, rondom nul, en buiten-ruimte in de omgeving. Terwijl dat verschil in wezen, objectief bezien dus, niet bestaat. Misschien is de cirkel die wij rondom een atoom denken, in wezen wel een rechte lijn met alleen maar links en rechts, bezien vanuit een gezichtspunt dat wij niet kennen.
Wij vinden een atoom zeer klein, maar dat is een waarde-oordeel. Immers voor zeer langzaam licht kan ons atoom de hele kosmos zijn.

Die eindige sfeer, als beperkt bewustzijn, als eindig licht, schept zelf het verschil, met als resultaat het ontstaan, of minstens de ervaring, van binnen-ruimte versus buiten-ruimte met dan natuurlijk ook grensgebieden tussen binnen en buiten.

En zo doet de werkelijkheid zich natuurlijk ook voor, ook als het gaat om atomen en wat er tussen en in hen speelt. Er bestaat hoe dan ook iets als binnen-ruimte in onze werkelijkheid, verborgen ruimte binnen de kernen van de atomen. Daar kunnen we nooit helemaal bij, alleen een oneindig licht kan dat.
We noemen die ruimte massa, de massa van neutronen en protonen, of de massa van quarks. Maar we weten niet wat we bedoelen met massa. Het is begrensde ruimte, dat weten we. En we kunnen het niet volledig bereiken, dat weten we ook. En het verzet zich tegen verandering van zijn snelheid. En we noemen die ruimte klein, maar dat is een waarde-oordeel. Dat is wat we weten.
Geconcentreerde of concentrerende binnen-ruimte, dat is eigenlijk de meest objectieve beschrijving van massa.

Er bestaat ook iets als buiten-ruimte in onze werkelijkheid, het veld van licht dat zich uitbreidt in de ruimte.

En dan bestaan er natuurlijk ook grensgebieden tussen binnen- en buiten-ruimte, daar waar elektronen rondom atomen, moleculen en dingen zweven en zwermen. En in die grensgebieden gebeurt alles. Leven is letterlijk oppervlakkig.

Nog enkele slotopmerkingen over neutronen, protonen en elektronen, in een poging om die deeltjes te schetsen.
Dit is mijn schets: Vóór het begin was licht wellicht oneindig snel, en ervaarde helemaal niets. Toen, in het begin, werd licht eindig snel, doordat het tijd nodig ging hebben . Vanaf dat moment was er verschil tussen hier en daar, en verleden en nu.
In dat beperkte gezichtsveld ontstonden ook gezichtspunten. Die gezichtspunten waren in het begin alleen zelf bewust, voelde slechts een relatie met hun binnen-ruimte, zoals neutronen doen.
Later echter, werden die gezichtspunten zich ook bewust van hun omgeving en dus van elkaar. Het neutron werd een proton-elektron paar, met niet alleen een relatie met de binnen-ruimte maar ook met de buiten-ruimte.
Vanaf dat moment werden grotere relatiepatronen mogelijk, grotere atomen, moleculen, dingen en zelfs levende wezens. Vanaf dat moment werd ook wiskunde mogelijk en natuurkunde en leven, als harmonie in de relaties.

Kunnen we ons zo'n creatief gezichtspunt voorstellen, dat uit slechts een verschil tussen binnen- en buiten-ruimte alle harmonie en schoonheid schept? Ik denk het, en misschien kunnen we het nog beter voelen. Bewogen en gegrepen worden door muziek, dat is ook begrijpen van muziek.

Dit is natuurlijk een kwalitatieve beschrijving van een atoom. Maar wat is daar verkeerd aan?
We geven altijd kwalitatieve beschrijvingen. Zelfs massa, lading, ruimte en tijd zijn al kwalitatieve begrippen. Zie meer daarover in deel II van de Relationele filosofie.

Overigens heeft de Nederlandse natuurkundige prof. H.B.G. Casimir in 1958 al een pleidooi gehouden voor afschaffing van de maatstaven gram en coulomb (Journal of Electronics and Control, Vol. 4, No. 5, p. 463, May 1958) waarin hij zich voorstelde dat kinderen in de toekomst naar de winkel gaan om bijvoorbeeld 1000000000000000000000000000 massa-eenheden spek te bestellen (±1,66 kg).

Jan Helderman
eind 1999 - begin 2000